【基礎から学ぶ直流回路】最大電力～最小定理の考え方

基本的に”イメージ”を意識した内容となっておりますので、基礎知識の無い方への入門向きです。
じっくり学んでいきましょう！

今回は、「最大電力」についての説明です。

最大電力

起電力E、内部抵抗rで構成される電源に抵抗Rを繋いだ時、抵抗Rに発生する電力が最大になる条件は内部抵抗r＝抵抗R。その時の最大電力P_m[W]はE²/4rとなる。

起電力E、内部抵抗rで構成される電源に抵抗Rを繋いだ時、抵抗Rに発生する電力が最大になる条件は内部抵抗r＝抵抗Rです。
では、何故内部抵抗r＝抵抗Rの時に電力が最大になるかを考えてみましょう。

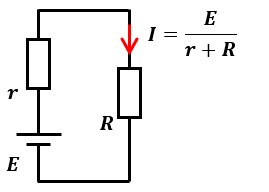
図1は、起電力E、内部抵抗rで構成される電源に抵抗Rを繋いだ回路です。
抵抗Rでの消費電力Pは以下のように表せます。

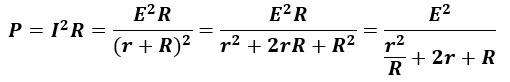
この式から、分母が小さければ小さい程電力が大きくなることがわかります。
つまり、分母が最小になる時に電力が最大になるということです。

分母を構成している中で変数はRのみなので、Rの値がいくつの時に分母が最小になるかを考えます。
分母の第2項の2rは定数ですので、変数であるRを含む分母の第1項r²/Rと第3項Rの和が最小の時に電力が最大になります。

突然ですが、「最小定理」をご存じでしょうか？
「2つの正の数(以降は2数と呼びます)があり、2数の積が一定である場合、2数が等しい時に2数の和が最小になる」という定理です。
以下に例を示します。

最小定理のイメージはできたかと思います。

何故唐突に最小定理の説明を始めたかというと、r²/RとRの2数にも最小定理が適用できるからです。

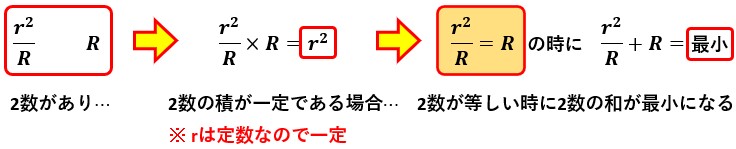
つまり、r²/R＝Rの時に分母が最小になり、電力が最大になります。
この式を整理するとr＝Rとなるので、抵抗Rに発生する電力が最大になる条件は内部抵抗rが抵抗Rと等しくなることだと言えます。

以上が、内部抵抗r＝抵抗Rの時に電力が最大になる理由です。

ちなみに、最大電力P_mはr＝Rの関係から以下のように表せます。

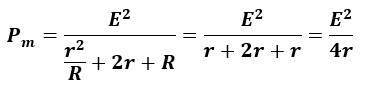
以上、「最大電力」についての説明でした。

【基礎から学ぶ直流回路】

Gadget Gate