今回は、「テブナンの定理」についての説明です。
複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電圧源に変換する方法。この方法で変換した回路を「テブナンの等価回路」と呼ぶ。
テブナンの定理
私は、学生の頃に鳳-テブナンの定理と習ったような気がします。
調べてみたところ、テブナンの定理は直流の時に成り立つことを証明したもので、同時期に鳳さんが交流の時でも成り立つことを発表した為、2人の名前を合わせて呼ぶこともあるそうです。
本記事では、あくまでテブナンの定理についての説明を行います。
複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電圧源に変換する方法がテブナンの定理です。
それに対し、複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電流源に変換する方法としてノートンの定理というものも存在します。
ここで説明するのはテブナンの定理だけですけどね。
実例を用いて説明していきます。
そもそも、複数の起電力と負荷を含む電気回路を単一の内部抵抗のある電圧源に変換すると言葉で言われても良くわからないと思いますので、まずは図1をご覧下さい。
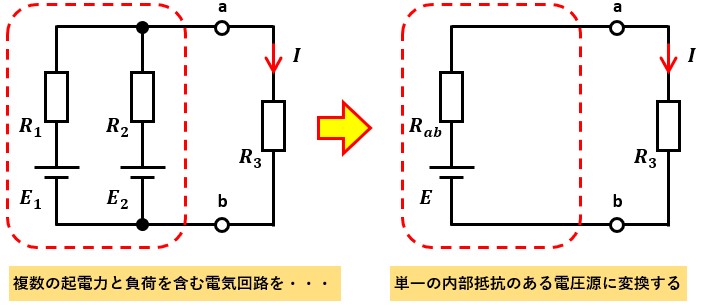
図1左側の電気回路をテブナンの定理に基づいて変換すると、図1右側のようになります。
図1右側の赤点線で囲った部分がテブナンの等価回路です。
変換方法は置いといて、とてもスッキリした回路を作れる定理なのだということがわかりますね。
本題である変換方法の説明に移ります。
図2の電流Iをテブナンの定理を用いて求めていきます。
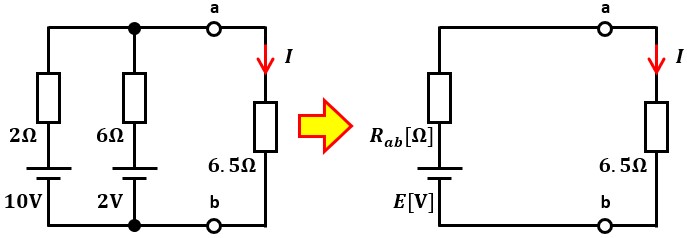
テブナンの等価回路は電圧源(起電力)Eと内部抵抗Rabにて構成されています。
ポイントは以下の通りです。
- テブナンの等価回路の起電力Eは、端子a-b間の電圧Vabに等しい。
- テブナンの等価回路の内部抵抗Rabは、電圧源を短絡除去した時のa-b間の合成抵抗に等しい。
まずは、テブナンの等価回路の起電力Eを求める方法についてです。
最初にテブナンの定理を適用したい回路(a-b間から向かって左側)を切り離します。
テブナンの等価回路の起電力Eは、端子a-b間の電圧Vabに等しいので、キルヒホッフの法則に則ってVabを計算します。
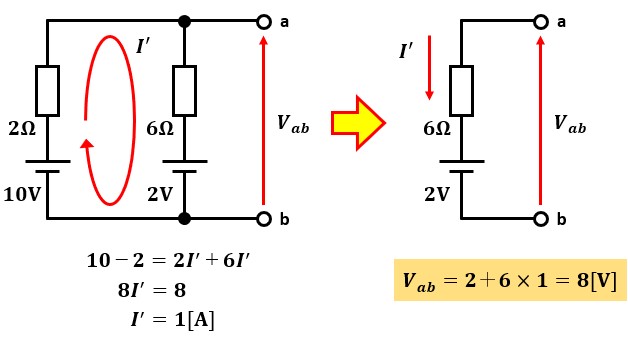
以上より、Vab=8[V]なので、テブナンの等価回路の起電力Eは8[V]となります。
抵抗の電圧降下の向きは電流の流れる向きと逆になりますので、注意して下さい。
次に、テブナンの等価回路の内部抵抗Rabを求める方法についてです。
最初にテブナンの定理を適用したい回路(a-b間から向かって左側)を切り離すのは起電力Eを求める際と同様です。
テブナンの等価回路の内部抵抗Rabは、切り離した回路から電圧源を短絡除去した時のa-b間の合成抵抗に等しいです。
短絡除去という言い方をすると難しそうですが、電源を無いものとして真っ直ぐに回路を繋ぐだけです。
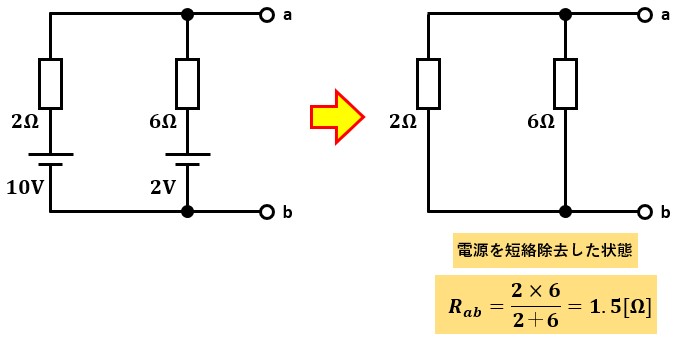
以上より、Rab=1.5[Ω]なので、テブナンの等価回路の内部抵抗Rabは1.5[Ω]となります。
並列回路の合成抵抗の求め方を忘れた方はこちらをご覧下さい。
テブナンの等価回路の構成要素であるE及びRabを求めたので、全体の回路は図5のようになります。
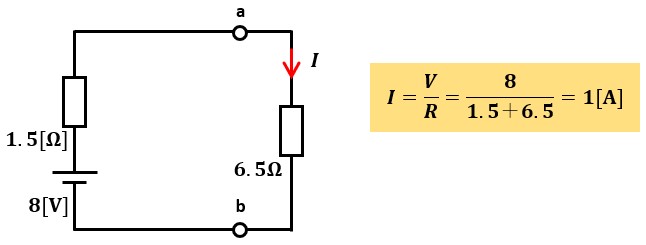
オームの法則より、電流I=1[A]と求めることができました。
以上がテブナンの定理を用いた変換方法です。
切り離した回路の端子間の電圧と合成抵抗を求めるとテブナンの等価回路ができる、と大まかに覚えておきましょう。
ちなみに、「キルヒホッフの法則」、「重ね合わせの理」、「ミルマンの定理」でも算出可能なので、併せて理解しておくと便利です。
以上、「テブナンの定理」についての説明でした。
【基礎から学ぶ直流回路】
◎抵抗の基礎 ~種類やカラーコードの見方
◎直列接続の考え方
◎並列接続の考え方
◎抵抗と並列に導線を繋いだ場合の電流の流れ
◎基準点による電位の変化
◎導体の電気抵抗 ~抵抗率と導電率の関係
◎キルヒホッフの法則
◎重ね合わせの理
◎テブナンの定理
◎ノートンの定理
◎テブナンの定理とノートンの定理の関係
◎ミルマンの定理
◎ブリッジ回路と平衡条件
◎ホイートストンブリッジ回路とメートルブリッジ回路
◎ブリッジ回路のΔ-Y変換
◎電圧源と電流源 ~等価電源と理想電源の違い
◎電圧源と電流源を含む回路の考え方
◎電圧源と電流源の接続方法の注意点
◎起電力と内部抵抗が等しい電圧源を複数並列に繋いだ場合の考え方
◎電力とジュールの法則
◎チップ抵抗器の定格電力と外形寸法表記
◎最大電力 ~最小定理の考え方
◎複数の電源から供給される電力の割合
