統計モジュール
統計モジュールは、データセットの統計を計算するための簡単な関数を提供します。 彼らは、NumPy、SciPy、またはSPSS、SAS、Matlabなどの他のソフトウェアと競合していないと主張しています。 そして確かに、それは非常に単純なモジュールです。 パラメトリック検定やノンパラメトリック検定は提供されません。 代わりに、いくつかの簡単な計算を行うために使用できます(ただし、Excelでも同じことができると思います)。 さらに、int、float、decimals、およびfractionsをサポートしていると主張しています。
統計モジュールは、(1)中央の場所の平均と測定値、(2)広がりの測定値、および(3)2つの入力間の関係の統計を測定できます。
Statistics.mean()
統計モジュールには、多数の関数が含まれています。 それぞれについては説明しませんが、そのうちのいくつかについて説明します。 この場合、データセットはリストに配置されます。 次に、リストが関数に渡されます。
整数の場合:
バツ = [1, 2, 3, 4, 5, 6]
平均 = 統計学。平均((バツ)。
印刷((平均)。
後者を実行すると、次のようになります。
分数の場合、用語は少し異なります。 分数と呼ばれるモジュールをインポートする必要があります。 また、分数を角かっこで囲み、その前に大文字のFを書き込む必要があります。 したがって、0.5はF(1,2)に等しくなります。 これは、大規模なデータセットでは実行できません。
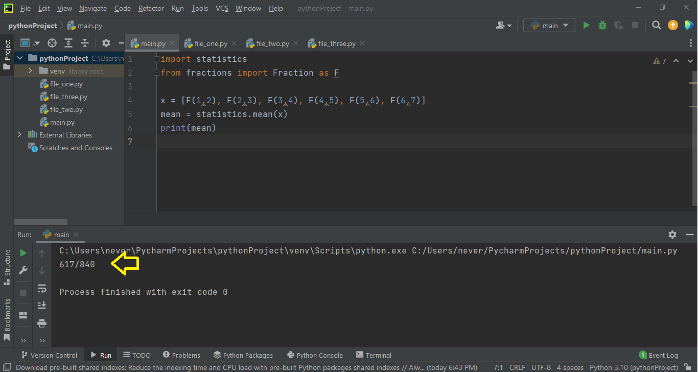
から 分数、 輸入 分数 なので F
バツ = [F(1,2), F(2,3), F(3,4), F(4,5), F(5,6), F(6,7)]
平均 = 統計学。平均((バツ)。
印刷((平均)。
後者を実行すると、次のようになります。
ほとんどの調査作業で遭遇する最も一般的なタイプの数値は10進値であり、統計モジュールを使用してこれを達成するのは非常に困難です。 最初にdecimalモジュールをインポートしてから、すべての10進値を引用符で囲む必要があります(これは、大きなデータセットがある場合はばかげて実用的ではありません)。
から 10進数 輸入 10進数 なので D
バツ = [D(“0.5”), D(“0.75”), D(“1.75”), D(“2.67”), D(“7.77”), D(“3.44”)]
平均 = 統計学。平均((バツ)。
印刷((平均)。
後者を実行すると、次のようになります。
2.813333333333333333333333333

統計モジュールは、平均、幾何平均、調和平均も提供します。 Statistics.median()とstatistics.mode()はstatistics.mean()に似ています。
Statistics.variance()およびstatistics.stdev()
研究では、サンプルサイズが非常に大きく、母集団のサイズとほぼ同じになることはめったにありません。 そこで、サンプルの分散とサンプルの標準偏差を見ていきます。 ただし、それらは母分散と母標準偏差も提供します。
繰り返しになりますが、小数を使用する場合は小数モジュールをインポートする必要があり、分数を使用する場合は分数モジュールをインポートする必要があります。 これは、統計分析の観点からすると、かなりばかげており、非常に非現実的です。
から 10進数 輸入 10進数 なので D
バツ = [D(“0.5”), D(“0.75”), D(“1.75”), D(“2.67”), D(“7.77”), D(“3.44”)]
var = 統計学。分散((バツ)。
印刷((var)。
後者を実行すると、次のようになります。
7.144266666666666666666666667
または、次のようにして標準偏差を計算することもできます。
から 10進数 輸入 10進数 なので D
バツ = [D(“0.5”), D(“0.75”), D(“1.75”), D(“2.67”), D(“7.77”), D(“3.44”)]
std = 統計学。stdev((バツ)。
印刷((std)。
後者を実行すると、次のようになります。
2.672876103875124748889421932
ピアソン相関
何らかの理由で、統計モジュールの作成者はANOVAテスト、t検定などを無視しましたが、相関と単純な線形回帰が含まれていました。 ピアソン相関は、データが正常である場合にのみ使用される特定のタイプの相関です。 したがって、これはノンパラメトリック検定です。 スピアマン相関と呼ばれる別のテストがあります。これは、データが正常でない場合にも使用できます(これは事実である傾向があります)。
バツ = [1.11, 2.45, 3.43, 4.56, 5.78, 6.99]
y = [1.45, 2.56, 3.78, 4.52, 5.97, 6.65]
corr = 統計学。相関((バツ、 y)。
印刷((corr)。
後者を実行すると、次のようになります。
線形回帰
単純な線形回帰が実行されると、次の式が実行されます。
y=勾配*x+切片
Excelもこれを行います。 ただし、このモジュールで実行できるほとんどのことは、勾配の値と、線を再作成できる切片を出力することです。 ExcelとSPSSは方程式に沿ったグラフを提供しますが、統計モジュールではそのどれも提供しません。
バツ = [1.11, 2.45, 3.43, 4.56, 5.78, 6.99]
y = [1.45, 2.56, 3.78, 4.52, 5.97, 6.65]
スロープ、 傍受 = 統計学。linear_regression((バツ、 y)。
印刷((「傾きは%sです」 % スロープ)。
印刷((「切片は%sです」 %インターセプト)。
印刷((“%sx +%s = y” % ((スロープ、 傍受)。)。
後者を実行すると、次のようになります。
スロープ は 0.9111784209749394
インターセプト は 0.46169013364824574
0.9111784209749394 x + 0.46169013364824574 = y
共分散
さらに、統計モジュールは共分散を測定できます。
バツ = [1.11, 2.45, 3.43, 4.56, 5.78, 6.99]
y = [1.45, 2.56, 3.78, 4.52, 5.97, 6.65]
cov = 統計学。共分散((バツ、y)。
印刷((cov)。
後者を実行すると、次のようになります。
Pythonは統計モジュールと呼ばれるモジュールを提供していますが、高度な統計用ではありません。 データセットを実際に分析したい場合は、統計モジュール以外のモジュールを使用してください。 シンプルすぎるだけでなく、Excelで提供されるすべての機能を簡単に見つけることができます。 さらに、このモジュールがテストに関して提供するテストは、ピアソン相関と単純線形回帰の2つだけです。 ANOVA、t検定、カイ2乗などはありません。 さらに、10進数を使用する必要がある場合は、10進数モジュールを呼び出す必要があります。これは、大規模なデータセットや非常に大規模なデータセットではイライラする可能性があります。 このモジュールを使用して実際の統計作業を行う必要がある人を捕まえることはできませんが(高度なものが必要な場合はSPSSを使用してください)、探しているのが単純な楽しみであれば、このモジュールはあなたにぴったりです。
ハッピーコーディング!
The post Pythonの統計モジュール appeared first on Gamingsym Japan.
