今回は、「整流形計器の平均値と実効値」についての説明です。
交流波形用の電圧計・電流計などのこと。
逆に、直流波形は測定できない。
整流形計器とは?
整流形計器とは、整流器と可動コイル形計器を組み合わせた計器のことです。
整流器は交流を直流に変換する(整流する)機器、可動コイル形計器は直流専用の電圧計・電流計などのことです。
要は、整流形で交流を直流に変換し、可動コイル形計器で直流を測定するのが整流形計器ということです。
整流器を介するので、逆に直流は測れません。
そんな整流形計器ですが、実際に測定するのは平均値であって実効値ではありません。
そこで、整流形計器は平均値から実効値を割り出して目盛表示するようにできています。
つまり、整流形計器を読み取った時に10[V]を示していたら、それは実効値の10[V]になっているのです。
整流形計器の問題点
整流形計器は、通常20~20kHz帯という広い範囲での測定が可能で、消費電力が少なく感度も良好だと言われています。
ただ、この感度が良いという点が逆に問題となる場面があります。
それは、測定する交流波形にノイズが乗ってひずんでいた場合です。
ひずみ部分まで細かく検知されてしまうので、誤差が大きくなってしまうということです。
なので、ひずんでいる交流波形の場合は整流形計器を用いるべきではありません。
近似実効値整流方式という補正機能を持った計器を使用しましょう。
ちなみに、データシートなどに整流方式の違いにより実効値(RMS)の他に平均値整流形(MEAN)というものが載っていることがあります。
この平均値整流形が整流形計器を指しています。
実際の実効値と差があるのはここで説明した内容によるものだということですね。
実際の考え方
今、目盛りが正弦波交流に対する実効値になる整流形の電圧系があったとして、図1のような方形波の電圧値を測定したとします。
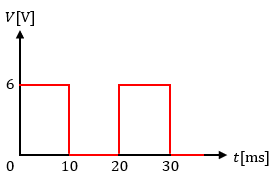
この時の整流形が指示する電圧値を計算で求めてみましょう。
整流形計器について思い出してほしいのですが、『実際に測定するのは平均値であって実効値では無い。平均値から実効値を割り出して目盛表示している。』と述べましたよね?
つまり、平均値を求めて、実効値に変換する必要があります。
なので、まずは平均値から割り出します。
10[ms]の間は6[V]、10[ms]の間は0[V]なので、平均すると(10×6+10×0)/20=3[V]になります。
まあ、方形波だし計算せずともわかりますよね。
ここで、波形率を適用します。
波形率は、波高率と共に「正弦波交流の平均値と実効値」で説明しています。
波形率=実効値÷平均値=1.11になるという関係です。
(※ 振幅Vの交流波形の実効値(V/√2)を平均値(2V/π)で割っただけだったりします。)
よって、実効値は平均値×1.11=3.33[V]ということになり、整流形計器が指示する電圧値は3.33[V]だとわかります。
地味に電験三種の過去問に出てきたことがありますので、受験を考えている方は覚えておくに越したことはないです。
以上、「整流形計器の平均値と実効値」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
