今回は、「重ね合わせの理」についての説明です。
2つ以上の起電力を含む回路の電流を、各起電力がそれぞれ単独にあるものと考えて別々に電流を求め、重ね合わせたものに等しくなる。
重ね合わせの理
実例を用いて説明していきます。
図1のように起電力が2つ含まれる電気回路があります。
この回路の電流Iを重ね合わせの理を用いて求めます。
起電力30[V]だからそのまま求めればいいとか考えないでくださいね?
まず、起電力が単独に存在する回路に分割します。
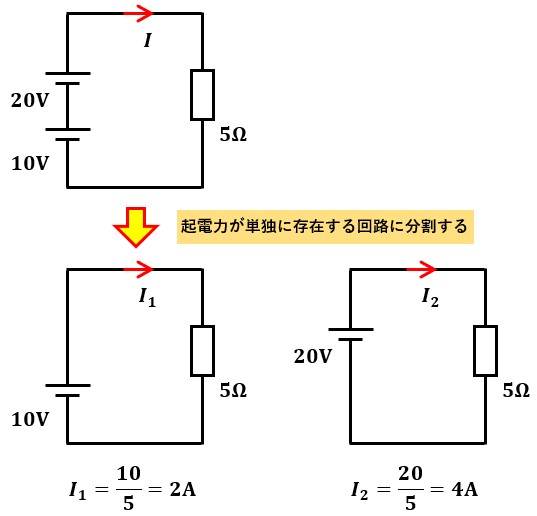
分割した回路ごとの電流I1及びI2を算出して重ね合わせたものが回路分割前の電流Iに等しくなりますので、I=I1+I2=2+4=6[A]と求めることができます。
このように、2つ以上の起電力を含む回路は重ね合わせの理を用いると理解しやすくなります。
仮に10V電源が反対方向に接続されていた場合、電流の流れる方向が異なることに注意です。
この場合、電流Iを正方向とすると、I=I1+I2=-2+4=2[A]となります。
ちなみに、「キルヒホッフの法則」、「テブナンの定理」、「ミルマンの定理」でも算出可能なので、併せて理解しておくと便利です。
以上、「重ね合わせの理」についての説明でした。
【基礎から学ぶ直流回路】
◎抵抗の基礎 ~種類やカラーコードの見方
◎直列接続の考え方
◎並列接続の考え方
◎抵抗と並列に導線を繋いだ場合の電流の流れ
◎基準点による電位の変化
◎導体の電気抵抗 ~抵抗率と導電率の関係
◎キルヒホッフの法則
◎重ね合わせの理
◎テブナンの定理
◎ノートンの定理
◎テブナンの定理とノートンの定理の関係
◎ミルマンの定理
◎ブリッジ回路と平衡条件
◎ホイートストンブリッジ回路とメートルブリッジ回路
◎ブリッジ回路のΔ-Y変換
◎電圧源と電流源 ~等価電源と理想電源の違い
◎電圧源と電流源を含む回路の考え方
◎電圧源と電流源の接続方法の注意点
◎起電力と内部抵抗が等しい電圧源を複数並列に繋いだ場合の考え方
◎電力とジュールの法則
◎チップ抵抗器の定格電力と外形寸法表記
◎最大電力 ~最小定理の考え方
◎複数の電源から供給される電力の割合
