今回は、「変調」についての説明です。
ひずみ波の使用例
周期性はあるけど正弦波ではないものをひずみ波と呼びます。
ひずみ波はいろんな周波数の波の塊というのは普通に理解できると思うのですが、そもそもひずみ波って何なのか疑問に持ちませんでしたか?
教科書に出てきたから一応覚えてはいるものの、どんなことに使用されているのかは謎という方は多いのではないでしょうか?
復調の説明に入る前にまずはそちらの補足説明から入ります。
電波などの情報は名前からわかる通り“波”です。
つまり、正弦波になっています。
電波の送信側と受信側があるとすると、通常時はただの正弦波が送受信されています。
この正弦波が届いている場合は“何も情報が無い”としています。
この“何も情報が無い”を伝える波に伝えたい情報の波を載せることで、通常時とは異なる波形を検出してデータを受信したことを検知しつつ内容を確認しています。
つまり、情報を伝える場合は複数の正弦波が混ざり合った波になるわけです。
これがひずみ波となる場合があるということです。
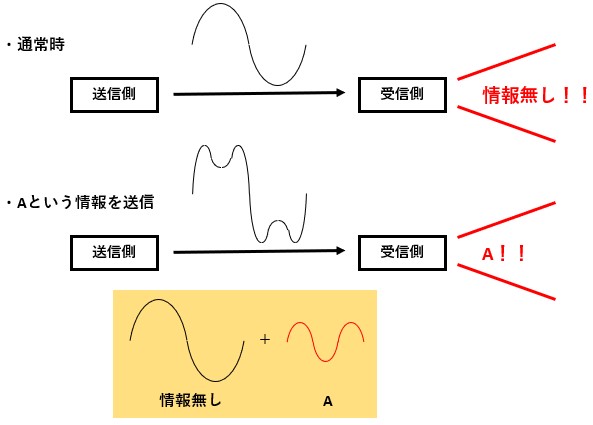
この伝えたい情報の波のことを信号波もしくは変調信号、”何も情報が無い”を伝えている信号を乗せるための波のことを搬送波・キャリア波、信号波と搬送波が合わさった波のことを変調波と呼びます。
そして、図1のように搬送波に信号波を乗せる操作を変調と呼びます。
例では描きやすいから搬送波の方を大きく・波長を長くしていますが、実際は搬送波の方が高周波になります。
この関係は、復調する際にコンデンサなどで構成した復調回路で搬送波を取り除くためのものです。
なぜ”何も情報が無い”ことを伝えているのかというと、おそらく問題無く通信できていることを相互に確認する為の基準として扱っているのではないかと思います。
基準が無いと正常な情報なのかノイズなのかわからなそうですし。
変調波の種類
変調波には、AM波・FM波・PM波という種類があります。
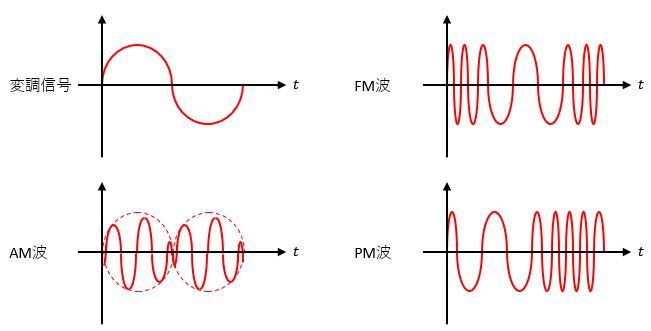
AMとは、Amplitude Modulationの略です。
意味は[振幅変調]になります。
普通に振幅変調波とも呼ぶ。
搬送波に対して振幅だけ変化します。
FMとは、Frequency Modulationの略です。
意味は[周波数変調]になります。
普通に周波数変調波とも呼ぶ。
搬送波に対して周波数だけ変化します。
周波数の逆数が位相なので、波形の疎密の周期がずれているだけでPM波と区別が付かない。
PMとは、Phase Modulationの略です。
意味は[位相変調]になります。
普通に位相変調波とも呼ぶ。
搬送波に対して位相だけ変化します。
位相の逆数が周波数なので、波形の疎密の周期がずれているだけでFM波と区別が付かない。
AM変調度と求め方
搬送波に信号波を乗せることで変調させるわけですが、その変調の度合・割合のことを変調度と呼びます。
中でもAM波の変調度であるAM変調度については公式から求めることが可能なので、紹介しておこうと思います。
AM変調度=
(振幅の最大値-振幅の最小値)/(振幅の最大値+振幅の最小値)
変調波の(山-谷)/(山+谷)になるということです。
単位は無いですが、パーセンテージで表示したい場合は×100をしましょう。
あくまで”度合”を示しているので必ず”1″以下になると覚えておけばそれなりに公式を忘れることはないのではないかと思います。
ちなみに、変調度を求める問題は電験三種の過去問にしれっと登場したことがあるので、受験するつもりの人は覚えておいた方が良いですよ?
以上、「変調」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
